"La música es la aritmética de los sonidos como la óptica es la geometría de la luz."
Claude Debussy.
(1862-1918.compositor francés y una figura central en la música europea de finales del siglo XIX y comienzos del siglo XX.)
Más allá de la percepción y el gusto, hay algo en la música que nos eleva. Es una elevación que no siempre responde a los caminos de los sentimientos o de las sensaciones. Es una elevación "racional".
Las neurociencias exploran hoy la relación entre el desarrollo de nuestro cerebro y las formas en las que aprendemos, pero también, la posibilidad de crear y de inventar. La música entonces, es una de las expresiones de la creatividad humana.
Ofrecemos, además de la experiencia auditiva, la experiencia racional de aprender acerca de la relación entre la música y el saber, y aún en un sentido más amplio, entre la música y el cerebro humano.
Entonces, los invitamos a escuchar, leer y volver a escuchar:
1) Preparación para la lectura: Escuchemos a Mozart.
2) Creatividad, ciencia y música: Mozart según Einstein.
3) Mozart y el misterio de la música. José A. Marina en: El Cultural. (Diario El Mundo) Madrid, España.
4) Música y Cerebro. Dr. F. J. Rubia (Real Academia Nacional de Medicina de la Universidad Complutense de Madrid.)
5) Mozart y la matemática. Por: Mario Palacios Campillo.
1- Preparación para la lectura: Escuchemos a Mozart.
En 1770, con tan solo 14 años, Mozart escuchó la obra Miserere Mei de Antonio Allegri e inmediatamente la transcribió al papel, de memoria, para luego hacerle correcciones menores en una segunda ocasión. Esta anécdota fue considerada prueba de su genialidad.
Wolfgang
Amadeus Mozart, (1756-1791) maestro del Clasicismo, considerado como uno de los
músicos más influyentes y destacados de la historia. Dotado de
una capacidad prodigiosa en el dominio de instrumentos de teclado y de violín. Con tan solo cinco
años ya componía obras musicales. A los diecisiete
años fue contratado como músico en la corte de Salzburgo, pero su inquietud le
llevó a viajar en busca de una mejor posición, siempre componiendo de forma
prolífica. Durante su visita a Viena en 1781, tras ser despedido
de su puesto en la corte, decidió instalarse en esta ciudad donde alcanzó la
fama que mantuvo el resto de su vida, a pesar de pasar por situaciones
financieras difíciles. En sus años finales, compuso muchas de sus sinfonías,
conciertos y óperas más conocidas, así como su Réquiem.
Réquiem (fragmento).
Mozart, Pequeña serenata nocturna.
2- Creatividad, ciencia y música: Mozart según Einstein.
El físico halló inspiración en
el compositor
El año pasado, el centenario de E=mc2 inspiró una
oleada de simposios, conciertos, ensayos y productos referidos a Albert Einstein. Este año, el mismo trato recibe otro genio,Wolfgang Amadeus Mozart nacido el 27 de
enero, doscientos cincuenta años atrás. Pero hay entre estos dos aniversarios
más coincidencias de las que podríamos pensar.
En una oportunidad, Einstein dijo que, mientras
Beethoven creó su música, la de Mozart "era tan pura, que parecía haber
existido en el universo desde siempre, esperando a ser descubierta por su dueño".
Einstein creía lo mismo respecto de la física, que más allá de las
observaciones y la teoría se encontraba la música de las esferas... que, según
escribió, revelaba "una armonía preestablecida", ya que expresaba
asombrosas simetrías.
Las leyes de la naturaleza, tal como las
de la teoría de la relatividad, estaban esperando que alguien con un oído
atento las recogiera del cosmos. Así, Einstein no atribuyó tanto sus teorías a
laboriosos cálculos, sino más bien al "puro pensamiento". Einstein
estaba fascinado con Mozart y percibía una afinidad entre los procesos
creativos de ambos, así como entre sus historias de vida. De niño, Einstein era
un alumno mediocre en la escuela.
Una válvula
de escape
La música era una válvula de escape de sus
emociones. A los 5 años empezó a tomar lecciones de violín, pero muy pronto las
prácticas le resultaron tan duras que le arrojó una silla a su profesora, quien
salió huyendo de la casa hecha un mar de lágrimas. A los 13, el físico
descubrió las sonatas de Mozart. El resultado fue una conexión casi mística,
dijo Hans Byland, amigo de Einstein desde el secundario. "Cuando su violín
empezó a cantar -le dijo Byland al biógrafo Carl Seelig-, las paredes de la habitación
parecieron alejarse... Por primera vez apareció ante mí Mozart en toda su
pureza, iluminado con las puras líneas de la belleza helénica, pícaro y
travieso, poderosamente sublime."
Desde 1902 hasta 1909, Einstein trabajó seis días
por semana en una oficina de patentes suiza, dedicando su tiempo libre a la
investigación en el campo de la física, su propia "travesura". Pero
la música también era su alimento, particularmente la música de Mozart, que se
encontraba en el núcleo de su vida creativa. Y así como las travesuras de
Mozart escandalizaron a sus contemporáneos, Einstein llevó en su juventud una vida notablemente bohemia. Su estudiada
indiferencia a la ropa y a su desgreñada melena oscura, junto con su amor por
la música y la filosofía, lo hacían más semejante a un poeta que a un
científico.
Tocaba el violín con pasión y con frecuencia lo
hacía en veladas musicales. Encantaba al público, particularmente a las
mujeres, una de las cuales llegó a firmar: "Tenía esa clase de belleza
masculina capaz de causar estragos". Einstein también coincidía con la
capacidad de Mozart de componer música magnífica, aun en condiciones de gran
dificultad y pobreza.
En 1905, el año en el que descubrió la
relatividad, Einstein vivía en un diminuto departamento y debía enfrentarse a
un matrimonio difícil y a dificultades de dinero. Esa primavera escribió cuatro
trabajos que estaban destinados a cambiar el curso de la ciencia y de las
naciones. Sus ideas sobre el espacio y el tiempo emergieron, en parte, del
descontento estético: le parecía que las asimetrías del campo de la física
ocultaban bellezas esenciales de la naturaleza; las teorías existentes carecían
de la "arquitectura" y de la "unidad interna" que él
hallaba en la música de Bach y de Mozart.
Contra la
complejidad
En sus luchas con enormes grados de complejidad
matemática, que lo condujeron a la enunciación de la teoría general de la
relatividad, en 1915, Einstein recurría con frecuencia, en busca de
inspiración, a la belleza simple de la música de Mozart.
"Siempre que se encontraba en un punto muerto
o en un momento difícil en su trabajo, buscaba refugio en la música -recordó su
hijo mayor Hans Albert-. Eso solía resolver todas sus dificultades."
Al final, Einstein sintió que en su propio campo
había logrado, como Mozart, desentrañar la complejidad del universo. Los
científicos suelen describir la teoría de la relatividad como la más bella que
se haya formulado nunca. El mismo Einstein siempre señaló la belleza de la
teoría: "Es difícil que alguien que la haya entendido verdaderamente sea
capaz de pasar por alto el encanto de esta teoría", dijo en una
oportunidad. La teoría es esencialmente la visión de un hombre de cómo debe ser
el universo. Y, sorprendentemente, el universo resultó ser muy parecido a como
Eisntein lo imaginó.
Su audaz matemática reveló fenómenos
espectaculares e inesperados como los agujeros negros.
Aunque era un gigante clásico, Mozart contribuyó a
sentar los fundamentos de los románticos con sus estructuras menos precisas. De
manera semejante, las teorías de la relatividad de Einstein completaron la era
de la física clásica y abrieron el camino para la física atómica y sus
ambigüedades. Al igual que la música de Mozart, la obra de Einstein es un hito
y un punto de partida.
En un concierto realizado en 1979 para celebrar el
centenario del nacimiento de Einstein, Julliard Qartet recordó haber tocado
para Einstein en su casa de Princeton, en Nueva Jersey (EE.UU.).
Habían llevado cuartetos de Beethoven y de Bartók
y dos quintetos de Mozart, según recordó el primer violinista Robert Mann,
cuyos comentarios fueron grabados por el académico Harry Woolf.
Después de interpretar a Bartók, Mann se dirigió a
Einstein: "Nos complacería mucho hacer música con usted". En 1952,
Einstein ya no tenía violín, pero los músicos habían llevado uno extra y
Einstein eligió el inquietante quinteto en Sol menor de Mozart. (Vídeo anexado por la cátedra.)
"El doctor Einstein casi no miraba las notas
de la partitura -recordó Mann-. Aunque sus manos, fuera de práctica, eran
frágiles, tenía una coordinación, un oído y una concentración
extraordinarios." Parecía, según su relato, extraer de la nada las
melodías de Mozart.
Por Arthur I.
Miller www.cienciaysaberXXI.edu.mx
3) Mozart y el misterio de la música. José A. Marina en: El Cultural. (Diario El Mundo) Madrid, España.
La música es un misterio, y la composición
musical un misterio dentro de un misterio, y la genialidad de Mozart un misterio dentro de un misterio
contenido en un misterio. O sea, que estoy por callarme. Pero llevo
tantos años investigando los mecanismos de la creatividad que caeré en la
tentación de contarles lo que los estudiosos de la invención -como Sloboda, que
es a mi juicio el mejor- y los propios músicos -como Strawinski , Schoenberg o
Session- han dicho acerca del arte de componer música. Recuerdo ahora unas
estupendas sesiones con Cristóbal Halfter mientras terminaba su Don Quijote, que me permitieron asistir casi en directo a la
creación de una obra.
El “caso Mozart” suscita dos preguntas: ¿Cómo componía? ¿Cómo pudo comenzar a crear tan pronto? A los seis años había compuesto minuetos, antes de cumplir los nueve su primera sinfonía, a los once su primer oratorio y a los doce su primera ópera. Seiscientas composiciones antes de morir a los 36 años. Una carrera breve, precoz y acelerada.
El esquema de la actividad creadora es siempre igual. Comienza con una ocurrencia que brota en la conciencia como una flor inesperada. Una frase, ritmo, melodía, un vago proyecto fruto sin duda de una elaboración inconsciente. No se asusten. Todas las actividades de nuestra inteligencia son inconsciente. Sólo conocemos algunos de sus resultados.
Mozart escribió: “No sé de dónde ni por qué me vienen las ideas, ni como puedo forzarlas a que vengan. Aparecen. Si me gustan, las retengo en la memoria. Y al final se van haciendo compatibles con las reglas del contrapunto o con las peculiaridades de los distintos instrumentos”.
Algo parecido dicen todos los creadores. “No puedo decirle cómo consigo mis temas: vienen sin pedir permiso”, confesaba Beethoven. Para Aaron Copland, el misterio de la creación musical es, precisamente, esa idea inicial: “Los temas llegan como un don celestial, en forma muy parecida a la escritura automática”.
Esas ocurrencias dependen de la memoria, es decir, están temporalmente fijadas. Mozart tenía ocurrencias de su tiempo. Todos los creadores que conozco -los verdaderos creadores, no los ingeniosos que se aprovechan de la moda del todo vale- tienen una memoria extraordinaria para lo suyo. Los alardes mnemotécnicos de Mozart forman parte de su leyenda.
Y una vez que se ha tenido esa primera idea, ¿qué sigue? Valèry decía: “El buen Dios -la Musa- nos da gratuitamente el primer verso. Pero a nosotros nos corresponde hacer el segundo, que debe rimar con éste y no ser indigno de él”. Hay que sacar provecho de ese accidente fortuito. Dicen que Mozart escribía de corrido, como si lo hiciera al dictado.
Es cierto que ha dejado menos borradores que Beethoven, cuyos cuadernos muestran que daba vuelta a las ideas durante años. Sin embargo, los facsímiles de La flauta mágica, publicados en 1979, nos presentan a un Mozart más trabajador. Durante la composición, cambió de tinta, y el color de la segunda se alteró rapidamente, por lo que podemos seguir la génesis de la obra.
Iba de lo general a lo particular. Como señala su biógrafo Einstein: “En una pieza de música de cámara o en una sinfonía, primero establece las voces principales, las líneas melódicas, del comienzo al final, saltando de un renglón a otro, e insertando las voces secundarias sólo cuando repasa o revisa el movimiento, en una segunda fase del procedimiento”.
En 1795, con 29 años, acabó de componer una serie de seis cuartetos para cuerda (K 387,421,428, 458, 464, 465). Durante tres años había estudiado la forma de componer de Haydn. Mozart se los dedicó, advirtiendo que eran “fruto de un largo y laborioso esfuerzo”. No hay genio improvisado.
Como no soy músico, ni crítico musical, me atrevo a decir que Haydn fue más innovador que Mozart, y que éste nos admira por su inexplicable precocidad. Fue un niño prodigio, y se ha convertido en paradigma de un fenómeno incomprensible. Sería por ello un estúpido si les dijera que tengo una explicación. Sospecho que en el fondo de todos los casos que he estudiado hay un cerebro con algunas capacidades especiales y sectoriales: una gran actividad -Mozart componía incluso cuando dormía, dice su biógrafo Turner-, un inagotable interés por un asunto, una capacidad de sintetizar muchos elementos, y una gran memoria.
David Feldman ha hecho el mejor estudio que conozco sobre niños prodigio. Lo que les caracteriza, una vez dadas esas facultades que he mencionado, comunes a todos los grandes creadores, es que atraviesan las etapas normales a una gran velocidad. Hayes ha documentado el hecho de que adquirir un elevado nivel de competencia en cualquier campo exige al menos diez años de trabajo intensivo, aún en el caso de individuos especialmente dotados, como Mozart. No olvidemos que hacer música no es tararear, sino utilizar una complejísima técnica. También él necesitoó esos diez años, lo que sucede es que estuvo en condiciones de comenzar la cuenta muy pronto.
Esto explica la necesidad de que el niño prodigio esté sometido a un proceso precoz e intensivo de aprendizaje. En el caso de Mozart, conocemos la abrumadora presencia de su padre, Leopold Mozart; su dedicación exclusiva a la carrera de su hijo. Por eso, los niños prodigio surgen con más frecuencia en sociedades expertas el objeto de su actividad.
Más del 50% de los prodigios en ajedrez de Estados Unidos provienen de tres áreas metropolitanas -Nueva York, San Francisco y Los ángeles- que tomadas en conjunto no abarcan más del 10% de la población del país. Se pueden encontrar porcentajes similarmente elevados de jóvenes violinistas en familias de origen judeo-rusas. Éste es un dato estimulante para los entusiastas de la educación, como soy yo.
El talento musical de Mozart quizá hubiera sido reconocido en cualquier época y cultura, pero es muy posible que se haya dado una especial conjunción entre su particular aptitud y el tipo de música que escuchó en su hogar.
Feldman lo resume en su libro Beyond Universals in Cognitive Development: “Concibo la aparición de un niño prodigio como la presencia en el tiempo de un ser humano excepcional y preorganizado, nacido y educado en un período posiblemente óptimo, y de un modo propicio para orientar sus intereses hacia el dominio de una esfera de conocimientos altamente evolucionada. En otras palabras, se produce una coincidencia, más asombrosa aún que los enormes talentos que la hicieron posible”.
Gardner, que también ha estado interesado en este asunto, añade algo más.El prodigio se da sobre todo en campos autónomos, que necesitan poca interacción con el mundo exterior, es decir, en actividades cerradas, autosuficientes, como el ajedrez, las matemáticas o la música.
La literatura es diferente. Con frecuencia, los niveles más altos en este campo se alcanzan en la madurez. Sería ridículo pensar que así se explica el misterio. Les aconsejo que olviden este artículo y escuchen la música de Mozart. Karl Barth, un estricto y arduo teólogo luterano, decía que en el Cielo se escucha a Bach, pero que de vez en cuando Dios se acerca de puntillas a escuchar a los ángeles, que siempre tocan música de Mozart.
El “caso Mozart” suscita dos preguntas: ¿Cómo componía? ¿Cómo pudo comenzar a crear tan pronto? A los seis años había compuesto minuetos, antes de cumplir los nueve su primera sinfonía, a los once su primer oratorio y a los doce su primera ópera. Seiscientas composiciones antes de morir a los 36 años. Una carrera breve, precoz y acelerada.
El esquema de la actividad creadora es siempre igual. Comienza con una ocurrencia que brota en la conciencia como una flor inesperada. Una frase, ritmo, melodía, un vago proyecto fruto sin duda de una elaboración inconsciente. No se asusten. Todas las actividades de nuestra inteligencia son inconsciente. Sólo conocemos algunos de sus resultados.
Mozart escribió: “No sé de dónde ni por qué me vienen las ideas, ni como puedo forzarlas a que vengan. Aparecen. Si me gustan, las retengo en la memoria. Y al final se van haciendo compatibles con las reglas del contrapunto o con las peculiaridades de los distintos instrumentos”.
Algo parecido dicen todos los creadores. “No puedo decirle cómo consigo mis temas: vienen sin pedir permiso”, confesaba Beethoven. Para Aaron Copland, el misterio de la creación musical es, precisamente, esa idea inicial: “Los temas llegan como un don celestial, en forma muy parecida a la escritura automática”.
Esas ocurrencias dependen de la memoria, es decir, están temporalmente fijadas. Mozart tenía ocurrencias de su tiempo. Todos los creadores que conozco -los verdaderos creadores, no los ingeniosos que se aprovechan de la moda del todo vale- tienen una memoria extraordinaria para lo suyo. Los alardes mnemotécnicos de Mozart forman parte de su leyenda.
Y una vez que se ha tenido esa primera idea, ¿qué sigue? Valèry decía: “El buen Dios -la Musa- nos da gratuitamente el primer verso. Pero a nosotros nos corresponde hacer el segundo, que debe rimar con éste y no ser indigno de él”. Hay que sacar provecho de ese accidente fortuito. Dicen que Mozart escribía de corrido, como si lo hiciera al dictado.
Es cierto que ha dejado menos borradores que Beethoven, cuyos cuadernos muestran que daba vuelta a las ideas durante años. Sin embargo, los facsímiles de La flauta mágica, publicados en 1979, nos presentan a un Mozart más trabajador. Durante la composición, cambió de tinta, y el color de la segunda se alteró rapidamente, por lo que podemos seguir la génesis de la obra.
Iba de lo general a lo particular. Como señala su biógrafo Einstein: “En una pieza de música de cámara o en una sinfonía, primero establece las voces principales, las líneas melódicas, del comienzo al final, saltando de un renglón a otro, e insertando las voces secundarias sólo cuando repasa o revisa el movimiento, en una segunda fase del procedimiento”.
En 1795, con 29 años, acabó de componer una serie de seis cuartetos para cuerda (K 387,421,428, 458, 464, 465). Durante tres años había estudiado la forma de componer de Haydn. Mozart se los dedicó, advirtiendo que eran “fruto de un largo y laborioso esfuerzo”. No hay genio improvisado.
Como no soy músico, ni crítico musical, me atrevo a decir que Haydn fue más innovador que Mozart, y que éste nos admira por su inexplicable precocidad. Fue un niño prodigio, y se ha convertido en paradigma de un fenómeno incomprensible. Sería por ello un estúpido si les dijera que tengo una explicación. Sospecho que en el fondo de todos los casos que he estudiado hay un cerebro con algunas capacidades especiales y sectoriales: una gran actividad -Mozart componía incluso cuando dormía, dice su biógrafo Turner-, un inagotable interés por un asunto, una capacidad de sintetizar muchos elementos, y una gran memoria.
David Feldman ha hecho el mejor estudio que conozco sobre niños prodigio. Lo que les caracteriza, una vez dadas esas facultades que he mencionado, comunes a todos los grandes creadores, es que atraviesan las etapas normales a una gran velocidad. Hayes ha documentado el hecho de que adquirir un elevado nivel de competencia en cualquier campo exige al menos diez años de trabajo intensivo, aún en el caso de individuos especialmente dotados, como Mozart. No olvidemos que hacer música no es tararear, sino utilizar una complejísima técnica. También él necesitoó esos diez años, lo que sucede es que estuvo en condiciones de comenzar la cuenta muy pronto.
Esto explica la necesidad de que el niño prodigio esté sometido a un proceso precoz e intensivo de aprendizaje. En el caso de Mozart, conocemos la abrumadora presencia de su padre, Leopold Mozart; su dedicación exclusiva a la carrera de su hijo. Por eso, los niños prodigio surgen con más frecuencia en sociedades expertas el objeto de su actividad.
Más del 50% de los prodigios en ajedrez de Estados Unidos provienen de tres áreas metropolitanas -Nueva York, San Francisco y Los ángeles- que tomadas en conjunto no abarcan más del 10% de la población del país. Se pueden encontrar porcentajes similarmente elevados de jóvenes violinistas en familias de origen judeo-rusas. Éste es un dato estimulante para los entusiastas de la educación, como soy yo.
El talento musical de Mozart quizá hubiera sido reconocido en cualquier época y cultura, pero es muy posible que se haya dado una especial conjunción entre su particular aptitud y el tipo de música que escuchó en su hogar.
Feldman lo resume en su libro Beyond Universals in Cognitive Development: “Concibo la aparición de un niño prodigio como la presencia en el tiempo de un ser humano excepcional y preorganizado, nacido y educado en un período posiblemente óptimo, y de un modo propicio para orientar sus intereses hacia el dominio de una esfera de conocimientos altamente evolucionada. En otras palabras, se produce una coincidencia, más asombrosa aún que los enormes talentos que la hicieron posible”.
Gardner, que también ha estado interesado en este asunto, añade algo más.El prodigio se da sobre todo en campos autónomos, que necesitan poca interacción con el mundo exterior, es decir, en actividades cerradas, autosuficientes, como el ajedrez, las matemáticas o la música.
La literatura es diferente. Con frecuencia, los niveles más altos en este campo se alcanzan en la madurez. Sería ridículo pensar que así se explica el misterio. Les aconsejo que olviden este artículo y escuchen la música de Mozart. Karl Barth, un estricto y arduo teólogo luterano, decía que en el Cielo se escucha a Bach, pero que de vez en cuando Dios se acerca de puntillas a escuchar a los ángeles, que siempre tocan música de Mozart.
4) Música y Cerebro. Dr. F. J. Rubia en la Real Academia Nacional de Medicina de la Universidad Complutense de Madrid
– 16 de abril de 2009
La música tiene un efecto conmovedor en nuestra psique. Sabemos que una determinada música puede calmarnos y otra puede tener el efecto contrario. Se ha utilizado en el pasado en la terapia de la epilepsia, en la enfermedad de Parkinson, para disminuir la presión arterial, en el tratamiento de niños afectados por el trastorno de hiperactividad con déficit de atención, en la depresión, en el tratamiento del estrés y en el insomnio.
El musicólogo y filósofo Julius Portnoy ha encontrado que la música puede cambiar las tasas metabólicas, aumentar o disminuir la presión arterial, los niveles de energía y la digestión de manera positiva o negativa dependiendo del tipo de música. La música puede aumentar la secreción de endorfinas por el cerebro y de esta manera producir placer así como relajación. Incluso se han hecho experimentos con plantas que crecieron más rápidamente que lo normal escuchando música clásica suave. Hay autores que han dicho que de todas las artes, la música es la que es capaz de modificar la consciencia de manera más poderosa.
El musicólogo y filósofo Julius Portnoy ha encontrado que la música puede cambiar las tasas metabólicas, aumentar o disminuir la presión arterial, los niveles de energía y la digestión de manera positiva o negativa dependiendo del tipo de música. La música puede aumentar la secreción de endorfinas por el cerebro y de esta manera producir placer así como relajación. Incluso se han hecho experimentos con plantas que crecieron más rápidamente que lo normal escuchando música clásica suave. Hay autores que han dicho que de todas las artes, la música es la que es capaz de modificar la consciencia de manera más poderosa.
Pero es más: se ha comprobado que la escucha por estudiantes de la Universidad de Wisconsin durante 10 minutos de la sonata en re mayor para dos pianos KV 448 tuvo efectos positivos en las pruebas de razonamiento espacio-temporal, efecto que duraba unos 10 minutos. A este fenómeno se le llamó el Efecto Mozart y los resultados de este estudio fueron publicados en la revista Nature en 1993.
La cuestión, pues, es: ¿cuáles son los mecanismos que pueden explicar estos efectos sobre nuestro cerebro?
Sabemos que el sonido incide sobre nuestro oído estimulando células situadas en el oído interno, células que traducen la energía mecánica en energía eléctrica, es decir, potenciales de acción, el único lenguaje que el cerebro entiende. Estos potenciales son todos iguales, provengan de la piel, de la retina del ojo o de las papilas gustativas de la lengua. Pero en el caso de los sonidos, los potenciales eléctricos, a través de vías específicas, llegan a la corteza cerebral auditiva primaria localizada en el lóbulo temporal. El cerebro clasifica los sonidos en bandas de frecuencia, en intensidades y duraciones, así como en graduaciones de frecuencia, intensidad y duración.
Sabemos que el sonido incide sobre nuestro oído estimulando células situadas en el oído interno, células que traducen la energía mecánica en energía eléctrica, es decir, potenciales de acción, el único lenguaje que el cerebro entiende. Estos potenciales son todos iguales, provengan de la piel, de la retina del ojo o de las papilas gustativas de la lengua. Pero en el caso de los sonidos, los potenciales eléctricos, a través de vías específicas, llegan a la corteza cerebral auditiva primaria localizada en el lóbulo temporal. El cerebro clasifica los sonidos en bandas de frecuencia, en intensidades y duraciones, así como en graduaciones de frecuencia, intensidad y duración.
Las células de la corteza auditiva primaria no sólo se excitan entre sí, sino que también utilizan la inhibición para simplificar la información acústica, aumentar los contrastes y suprimir los ruidos de fondo. No hay que olvidar que el cerebro está sólo interesado en cambios y contrastes. Un sonido igual y constante termina por no oírse, gracias a dos fenómenos: la adaptación de los receptores y un proceso inhibitorio llamado habituación. Tampoco le interesa al cerebro la frecuencia exacta de un sonido. Cualquier violinista puede cambiar su nota ‘la’ media de 440 a 450 herzios y el cerebro se adapta inmediatamente a ese cambio. Como se mostrado, somos sordos respecto a las frecuencias exactas de los tonos, al cerebro le interesan las distancias relativas entre las frecuencias más que las frecuencias absolutas. Esto es válido para todos los sentidos. En la visión, la luminosidad absoluta no es interesante para el cerebro, sino sólo los contrastes.
Por otra parte el cerebro no es ningún órgano pasivo. Envía fibras hacia las células sensoriales del oído interno controlando su sensibilidad. Y también participa activamente en los diversos escalones que recorre la información auditiva, modificando y filtrando esa información. Esto quiere decir que los tonos que percibimos no existen en la Naturaleza, sino que son atribuciones que la corteza cerebral asigna a las señales eléctricas que le llegan desde la periferia, interviniendo además en cada uno de las estaciones de relevo, desde el oído hasta el lóbulo temporal. Sin este sistema centrífugo, el efecto llamado de “cocktail party”, o sea la capacidad de escuchar una conversación en una fiesta, a pesar del ruido de fondo, sería imposible. El cerebro no se contenta con el análisis de los sonidos, sino que se preocupa más bien de la interpretación activa de esos sonidos.
La corteza auditiva primaria está rodeada de la llamada corteza auditiva secundaria, y ésta a su vez de la corteza auditiva terciaria . Mientras que la corteza auditiva primaria se concentra en las características de tonos aislados, la corteza auditiva secundaria es responsable de la relación entre varios tonos. La corteza auditiva del hemisferio derecho del cerebro se concentra en tonos simultáneos y analiza las relaciones armónicas entre ellos. La corteza auditiva secundaria del hemisferio izquierdo se concentra en la relación entre secuencias de tonos, por lo que es importante para la percepción del ritmo.
La melodía no es simplemente una secuencia de tonos, sino que éstos varían en ella de frecuencia y acento, provocando en el cerebro sensaciones únicas. Melodía, ritmo y armonía combinados forman la música.
Nuestra capacidad para percibir música es muy temprana. Incluso recién nacidos reaccionan a estímulos musicales, y con un mes, el bebé puede discriminar ya tonos de diferentes frecuencias. Con seis meses se habla ya de una ‘musicalidad’ desarrollada. Y a los tres o cuatro años, los niños comienzan a reproducir la música de la cultura en la que están inmersos. Ahora bien, un entendimiento pleno de la armonía se desarrolla como muy temprano a la edad de doce años.
La música es un medio de comunicación como lo es el lenguaje. Al igual que en el lenguaje, donde las distintas características (semántica, nombres de instrumentos, de frutos y de animales, prosodia, identificación de fonemas, etc.) están localizadas en diferentes partes del cerebro, en la música ocurre lo mismo, es decir, que, por ejemplo, la melodía y la localización de los tonos se localizan preferentemente en el hemisferio derecho. Por eso, en operaciones quirúrgicas, donde una parte del lóbulo temporal derecho tuvo que ser extirpado para evitar ataques epilépticos intratables con medicamentos, el paciente tuvo problemas con la percepción de la melodía, mientras que en operaciones similares con extirpación del las mismas regiones del lóbulo temporal izquierdo este problema no apareció. El análisis armónico parece ser también función de las regiones auditivas del hemisferio derecho. Curiosamente, los músicos profesionales utilizan más en la percepción de las melodías el hemisferio izquierdo y se ha comprobado que con el entrenamiento en música, la dominancia cerebral para la percepción de la melodía se desplaza del hemisferio derecho al hemisferio izquierdo
El hemisferio izquierdo es asimismo más apropiado para la percepción del ritmo. Esto indica que la percepción de la armonía y la percepción del ritmo utilizan áreas distintas del cerebro. Los músicos saben muy bien que hay personas que tienen una capacidad de percepción armónica brillante, pero son poco dotados para la percepción del ritmo y viceversa.
El análisis con modernas técnicas de imagen cerebral, como la tomografía por emisión de positrones o la resonancia magnética funcional han mostrado que el sustrato neurológico del lenguaje y de la música se solapan. Se ha podido comprobar, como hemos dicho, que el hemisferio derecho atiende a los aspectos melódicos de la música y el izquierdo a los aspectos rítmicos. Las estructuras del sistema emocional o límbico que procesan las emociones en el hemisferio derecho se activan cuando sujetos voluntarios se imaginan la música. El hemisferio derecho también es más sensible para la armonía.
En músicos profesionales con oído absoluto se ha podido constatar que tienen un plano temporal más grande que en personas normales. El plano temporal es una región del lóbulo temporal que es importante para la comprensión del lenguaje. Asimismo, la mitad anterior del cuerpo calloso, que une ambos hemisferios, también es mayor en músicos que comenzaron su entrenamiento antes de los siete años de edad, que en personas normales. Una característica típica en músicos profesionales es que utilizan menos regiones cerebrales cuando ejecutan movimientos con la mano que las personas normales.
El canto, que implica tanto la música como el lenguaje, parece involucrar ambos hemisferios si hay palabras por medio, pero el canto sin palabras depende más del hemisferio derecho.
Respecto al sexo, parece bien establecido que la lateralización de funciones en los hemisferios es más acusada en el hombre que en la mujer. Las diferencias en tareas verbales, matemáticas, sociales y visuo-espaciales (orientación en el espacio guiada por la visión) entre hombre y mujer se deben en parte a esas diferencias en la lateralización de funciones. Personas entrenadas musicalmente muestran diferencias: mientras que en hombres el hemisferio derecho es dominante para analizar secuencias de tonos, en mujeres son ambos hemisferios los implicados.
Respecto al sexo, parece bien establecido que la lateralización de funciones en los hemisferios es más acusada en el hombre que en la mujer. Las diferencias en tareas verbales, matemáticas, sociales y visuo-espaciales (orientación en el espacio guiada por la visión) entre hombre y mujer se deben en parte a esas diferencias en la lateralización de funciones. Personas entrenadas musicalmente muestran diferencias: mientras que en hombres el hemisferio derecho es dominante para analizar secuencias de tonos, en mujeres son ambos hemisferios los implicados.
Una cuestión importante es la del origen de la música. En el libro de Charles Darwin de 1871 “El origen del hombre y la selección en relación al sexo”, éste decía: “parece probable que los progenitores del hombre, sean hombres o mujeres, o ambos sexos, antes de adquirir el poder de expresar el amor mutuo en lenguaje articulado, intentaron hechizarse uno al otro con notas musicales y ritmo”. Darwin se dio cuenta de la ubicuidad de la música en todas las culturas conocidas, el desarrollo espontáneo de las capacidades musicales en los niños y la manera en la que provoca fuertes emociones, antes de concluir: “Todos estos hechos con respecto a la música y al lenguaje apasionado se hacen inteligibles hasta cierto punto si asumimos que los tonos musicales y el ritmo se utilizaron por nuestros antecesores semihumanos durante el período del cortejo”.
Tanto la música como el lenguaje están presentes en todas las sociedades humanas que hoy existen, y los arqueólogos afirman que ambas estuvieron también presentes en las sociedades prehistóricas. Ambas poseen una estructura jerárquica que consiste en elementos acústicos, palabras o tonos respectivamente, que se combinan para formar frases, expresiones o melodías, aunque la naturaleza de esas unidades es diferente en el lenguaje, que son símbolos, mientras que en la música no. El lenguaje, sea hablado, escrito o por gestos, se utiliza como medio de comunicación de ideas o conocimientos; la música, sin embargo, es un sistema de comunicación no referencial, y aunque no nos comunique nada sobre el mundo, puede tener y tiene un impacto profundo sobre nuestras emociones.
Por tanto, o el lenguaje se deriva de la música, o ambos, lenguaje y música se desarrollaron en paralelo, o existió un precursor de ambos, una especie de ‘musilenguaje’, como así se le ha llamado.
El músico ruso Vissarion Shebalin , el año 1953, a la edad de 51 años, sufrió un derrame cerebral en el lóbulo temporal izquierdo que le paralizó la mano derecha, la parte derecha de la cara y trastornó el lenguaje, pero su labor de compositor continuó sin problemas, terminando su quinta sinfonía en 1963, poco antes de su tercer ataque de apoplejía que lo llevó a la tumba. El neuropsicólogo ruso Alejandro Luria informó sobre este caso en el Journal of Neurological Science en 1965 diciendo que era una prueba de que la música y el lenguaje eran dos sistemas separados en el cerebro.
El músico ruso Vissarion Shebalin , el año 1953, a la edad de 51 años, sufrió un derrame cerebral en el lóbulo temporal izquierdo que le paralizó la mano derecha, la parte derecha de la cara y trastornó el lenguaje, pero su labor de compositor continuó sin problemas, terminando su quinta sinfonía en 1963, poco antes de su tercer ataque de apoplejía que lo llevó a la tumba. El neuropsicólogo ruso Alejandro Luria informó sobre este caso en el Journal of Neurological Science en 1965 diciendo que era una prueba de que la música y el lenguaje eran dos sistemas separados en el cerebro.
Si realmente la música y el lenguaje están separados, ¿existe también la posibilidad que se de el lenguaje sin la música? Efectivamente esto es así. Se han referido casos de amusia, o sea, incapacidad de entender y/o producir música, pero con conservación del lenguaje. Sin embargo, también puede producirse una afectación tanto del lenguaje como de la música. El compositor francés Maurice Ravel, que en 1927 empezó a escribir tonterías, y en 1928 tocando su Sonatina en Madrid, saltó desde el primer tiempo al final, mostró muchas dificultades en la motricidad y en el lenguaje, así como se vio impedido para escribir o tocar una sola nota de música. En este caso, ambos sistemas, la música y el lenguaje, se vieron afectados. A fin de cuentas, en el canto, lenguaje y música están unidos.
Los pacientes que sufren de amusia, o sea incapacidad para percibir la música, mientras su capacidad lingüística permanezca intacta suelen tener lesiones en los lóbulos temporales derecho o izquierdo. Sin embargo, los que mantienen su capacidad musical, pero pierden las lingüísticas, suelen sufrir lesiones sólo en el lóbulo temporal derecho.
Se sabe que en el lenguaje, la sintaxis, la semántica, el análisis de los fonemas o la prosodia se localizan en lugares distintos del cerebro. Igualmente, en la música la melodía, el timbre o el ritmo también ocupan lugares distintos pudiendo sufrir un paciente con lesión cerebral la pérdida de uno de estos componentes, conservando los demás.
Un caso especial que muestra la separación de música y lenguaje en el cerebro desde épocas muy tempranas de la vida es el de los llamados ‘músicos sabios’, niños que son muy deficientes en sus capacidades lingüísticas, pero que tienen una musicalidad normal, o incluso excelente, como ocurre, por ejemplo, en el síndrome de Williams, al que me referí en mi comunicación en este mismo lugar hace dos años. Estos músicos sabios poseen capacidades con las que cualquier persona puede soñar: un oído absoluto, una percepción finísima, una capacidad enorme de representación acústica, y una memoria musical excepcional. Suelen tener estos músicos sabios lesiones en el hemisferio izquierdo, por lo que se supone que se desinhiben funciones del hemisferio derecho.
¿Cuándo se desarrolla la capacidad musical en los niños? Pues bien, existe una gran cantidad de trabajos experimentales que indican que antes de alcanzar la edad de un año, los niños ya poseen todas las capacidades de percepción musical que tienen los adultos normales, es decir, que no son músicos profesionales. Esto parece indicar que la música es un campo en el que el niño posee ya una competencia innata para ella, similar a la del lenguaje.
¿Cuál sería, pues, el valor de supervivencia de la música para haber desarrollado una capacidad innata a lo largo de la evolución? Evidentemente, aquí nos basamos en la especulación y algunos autores han propuesto que la música incrementa los lazos sociales fomentando las respuestas emocionales conjuntas cuando se danza o canta, aparte de poder relajar tensiones en los individuos. Algunos autores argumentan que es posible que la música se remonte al Homo erectus, es decir, a una época entre 1,8 millones y 300.000 años antes de nuestra era.
¿Cuál sería, pues, el valor de supervivencia de la música para haber desarrollado una capacidad innata a lo largo de la evolución? Evidentemente, aquí nos basamos en la especulación y algunos autores han propuesto que la música incrementa los lazos sociales fomentando las respuestas emocionales conjuntas cuando se danza o canta, aparte de poder relajar tensiones en los individuos. Algunos autores argumentan que es posible que la música se remonte al Homo erectus, es decir, a una época entre 1,8 millones y 300.000 años antes de nuestra era.
Esta opinión parece exagerada. Sabemos que nuestra especie, el Homo sapiens, hizo su aparición en la Tierra hace unos 200.000 años, pero que la explosión cultural que, probablemente llevó al lenguaje, a la aparición del arte y la religión, tuvo lugar hace unos 50.000 años. Y la hipótesis que hoy se maneja para explicar este retardo de 150.000 años en la aparición de esa explosión cultural es que fue motivada por una mutación. Las estrechas conexiones de la música con el lenguaje nos hacen pensar que muy probablemente su aparición en el ser humano es más reciente y dentro del período de existencia de nuestra propia especie. A favor de esta opinión estaría el hecho de que los registros arqueológicos indican que los instrumentos musicales hacen su aparición con el Homo sapiens.
Pero hay opiniones, como las del lingüista Steven Pinker, que se inclinan por pensar que la música es una “auditory cheesecake”, o sea, una delicia auditiva, algo marginal en la evolución, que, en el mejor de los casos es adaptativa al promover una solidaridad del grupo.
Tanto el lenguaje como la música tienen una estrecha relación con el movimiento, por lo que se considera que la música establece relaciones entre distintas funciones cerebrales, relaciones que también son consideradas características de nuestra especie. La música facilitaría este tipo de relaciones entre funciones distintas, tales como las emociones, la prosodia de nuestro lenguaje, la relación entre madre e hijo en ese proto-lenguaje casi musical que se emplea para establecer contacto entre una y otro, así como en la motricidad asociada a la periodicidad de los movimientos.
Tanto el lenguaje como la música tienen una estrecha relación con el movimiento, por lo que se considera que la música establece relaciones entre distintas funciones cerebrales, relaciones que también son consideradas características de nuestra especie. La música facilitaría este tipo de relaciones entre funciones distintas, tales como las emociones, la prosodia de nuestro lenguaje, la relación entre madre e hijo en ese proto-lenguaje casi musical que se emplea para establecer contacto entre una y otro, así como en la motricidad asociada a la periodicidad de los movimientos.
Con respecto a la posibilidad por muchos autores aceptada de la predisposición genética para la música, habría que suponer también la heredabilidad de esta facultad. Y, en efecto, se ha calculado que aproximadamente la mitad de los grandes compositores han tenido músicos profesionales en sus familias o descendían de familias con una larga tradición musical, como es el caso de la familia de Johann Sebastian Bach, que en siete generaciones se han contado hasta 64 profesionales de la música.
No quisiera terminar sin mencionar uno de nuestros misterios más grandes: la inspiración. ¿Qué han dicho los compositores famosos sobre esa misteriosa inspiración que les llevaba a plasmar en el papel su música? Pues en términos generales, que la música fluía de sus cabezas sin ningún problema. Richard Wagner lo comparaba como el fluir de la leche en una vaca, Saint-Saëns con un árbol de manzanas produciendo sus frutos y Mozart, tan soez como siempre, con una cerda orinando. Precisamente Mozart hablaba de que sus ideas musicales se le presentaban cuando estaba solo, cuando iba de una ciudad a otra en su carruaje o cuando no podía dormir por las noches. Su barbero se quejaba que tenía que andar siempre detrás de él para afeitarle porque se levantaba de pronto del cembalo para ir al escritorio a escribir la música. Tanto él como Robert Schumann oían la música, al parecer, completa en su cabeza antes de pasarla al papel.
A veces, la inspiración era sentida como una experiencia religiosa. Un criado encontró un día a Händel llorando a lágrima viva cuando en un maratón de 24 días escribió su “Mesías”. Y expresaba esta experiencia diciendo: “Veía el cielo abierto ante mí y al propio Dios Padre”. O Johannes Brahms que lo expresaba así: “Me sentía en consonancia con la eternidad, no hay nada más apasionante”.
Muchos compositores sufrían de lo que hoy podíamos llamar períodos mánicos o mánico-depresivos. Curiosamente, este tipo de enfermos muestran a veces altos valores de creatividad. Se supone que aproximadamente un tercio de todos los escritores y artistas, así como la mitad de los poetas, tuvieron síntomas mánico-depresivos. Los psicólogos sospechan que a este grupo pertenecen compositores como Berlioz, Bruckner, Gesualdo, Glinka, Händel, di Lasso, Mahler, Mussorgsky, Rachmaninoff, Rossini, Schumann, Tchaikowsky, etc.
Muchos compositores sufrían de lo que hoy podíamos llamar períodos mánicos o mánico-depresivos. Curiosamente, este tipo de enfermos muestran a veces altos valores de creatividad. Se supone que aproximadamente un tercio de todos los escritores y artistas, así como la mitad de los poetas, tuvieron síntomas mánico-depresivos. Los psicólogos sospechan que a este grupo pertenecen compositores como Berlioz, Bruckner, Gesualdo, Glinka, Händel, di Lasso, Mahler, Mussorgsky, Rachmaninoff, Rossini, Schumann, Tchaikowsky, etc.
Todos estos hechos no hacen más que corroborar la opinión de que nuestro cerebro emocional es mucho más importante no sólo para nuestra propia supervivencia sino también para estas funciones inconscientes de la creatividad,. Ahora sabemos lo que deberíamos haber intuido hace tiempo simplemente observando la evolución del cerebro: que las emociones son la base incluso de nuestro pensamiento racional.
Volviendo al comienzo de mi comunicación quisiera decir que la música despierta en lo seres humanos, sobre todo en aquellos que la aman, efectos conmovedores y placeres inefables. Y esto es así, y será así por mucho que progresemos en nuestros todavía precarios conocimientos sobre su organización cerebral. Estas consideraciones han sido precisamente el motivo de organizar un acto como el de hoy.
Bibliografía
Jourdan, R.
Music, the Brain and Ecstasy
Avon Books
New York, 1997
Sacks, O.
Musicophilia
Tales of Music and the Brain
Alfred A. Knopf
New York, 2007
Shaw, G. L.
Keeping Mozart in Mind
Academia Press
San Diego, Ca., 2000
Store, A.
Music and the Mind
Ballantine Books
New York, 1992
Wallin, N. L., Merker, B., and Brown, S. (Eds..)
The Origins of Music
Bradford Book
MIT Press
Cambridge, Mass., 2001
Jourdan, R.
Music, the Brain and Ecstasy
Avon Books
New York, 1997
Sacks, O.
Musicophilia
Tales of Music and the Brain
Alfred A. Knopf
New York, 2007
Shaw, G. L.
Keeping Mozart in Mind
Academia Press
San Diego, Ca., 2000
Store, A.
Music and the Mind
Ballantine Books
New York, 1992
Wallin, N. L., Merker, B., and Brown, S. (Eds..)
The Origins of Music
Bradford Book
MIT Press
Cambridge, Mass., 2001
5) Mozart y la matemática. Por: Mario Palacios Campillo.
La relación de la Música y las Matemáticas se remonta a la antigüedad; ya Pitágoras estudió estas influencias. Pero hasta Mozart no queda palpable esta relación: la del cálculo de probabilidades y la melodía. Mozart era un matemático en potencia y manejaba conceptos abstractos matemáticos, aunque de forma inconsciente, y así, al estudiar su obra se encuentran relaciones curiosas con las Matemáticas, como por ejemplo el número Pi, las Homotecias y la combinatoria (un apartado del cálculo de probabilidades).
Componer música es el arte de combinar distintas ideas musicales buscando una unidad formal. Si el desarrollo de las ideas es largo, mas costará combinarlas.
Así Mozart a los 21 años, en 1777, describe un juego de dados al cual va a asociar una pequeña obra musical. Era un vals de 16 compases, que tituló Juego de Dados Musical para escribir valses con la ayuda de dos dados sin ser músico ni saber nada de composición (K294). Decía sobre la composición musical que “Todo está compuesto, pero no escrito todavía”.
Minueto (juego de dados) de Mozart.
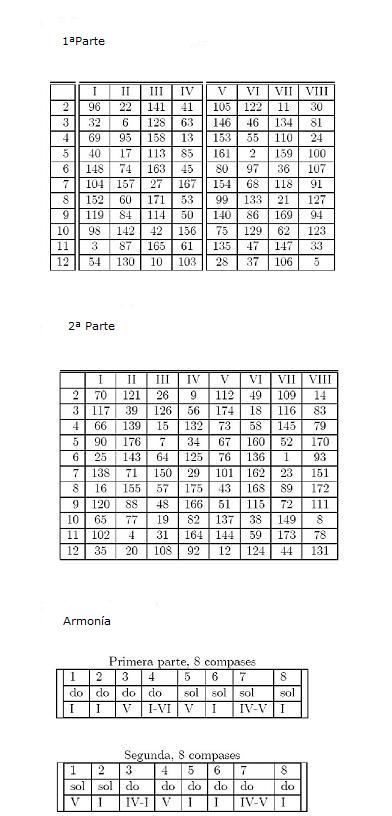
Cada uno de los compases se escoge lanzando dos dados y anotando la suma del resultado. Tenemos 11 resultados posibles( del 2 al 12). Mozart diseñó dos tablas: una para la primera parte del vals y otra para la segunda. Cada parte consta de 8 compases. Para obtener cada uno de los primeros compases( numerados del I al VIII) se lanza un par de dados y se anota la suma de puntos obteniéndose 8parejas: (n1, I), (n2, II), (n3, III), (n4,IV), (n5,V), (n6,VI), (n7,VII) y (n8,VIII).Cada pareja se asocia a un número de compases generándose ocho:N1, N2, N3, N4, N5, N6, N7 y N8.
Los 8 compases siguientes del vals se obtienen de forma similar:
(m1, I), (m2, II), (m3, III), (m4,IV), (m5,V), (m6,VI), (m7,VII) y (m8,VIII).
Cada pareja se asocia a un número generándose los otros ocho compases M1, M2, M3, M4, M5, M6, M7y M8.
Se generan así 3800 billones de valses distintos (con una duración aproximada de 30 seg) que si se tocaran de forma continua durarían aproximadamente 361 millones de años.
Mozart compuso 176 compases.La Tabla de los ocho primeros compases y la segunda del vals de Mozart están en la imagen. Mozart designó los compases por columna siguiendo un patrón sencillo de su época(Los amantes de la música pueden estudiar estos compases en otros propiamente musicales).
Ello nos lleva a una composición cuya armonía está en la imagen.
Ahora visto lo que hizo Mozart, podemos hacer una prueba: los Músico-Matemáticos( o ayudados) tiran los dados………….. .Como puede verse nadie duda que Mozart era un genio( ya sabía que componer era sólo pura Combinatoria).
"Teoría de la Probabilidad en la Composición Musical Contemporánea" de Susana Tiburcio. AMJ, Febrero de 2011.






















